-- load up the data: sa: load foaf-example-in-sw.sw -- first, we need a list of objects of interest: sa: |list> => |Dan> + |Libby> + |Craig> + |Liz> + |Kathleen> + |Damian> + |Martin> + |organisation: ILRT> + |organisation: Netgates> -- now show the table: sa: table[name,where-live,lives-with,email,works-for,website] "" |list> +------------------------+---------------------------+--------------+----------------------------------+------------------------+---------------------------------+ | name | where-live | lives-with | email | works-for | website | +------------------------+---------------------------+--------------+----------------------------------+------------------------+---------------------------------+ | Dan | UK: Bristol: Zetland road | Libby, Craig | email: danbri@w3.org | organisation: ILRT | | | Libby | | | email: libby.miller@bris.ac.uk | organisation: ILRT | | | Craig | | | email: craig@netgates.co.uk | organisation: Netgates | | | Liz | UK: Bristol | Kathleen | | organisation: Netgates | | | Kathleen | | | | organisation: Netgates | | | Damian | UK: London | | | | | | Martin | | | email: m.l.poulter@bristol.ac.uk | | | | organisation: ILRT | | | | | url: http://ilrt.org/ | | organisation: Netgates | | | | | url: http://www.netgates.co.uk/ | +------------------------+---------------------------+--------------+----------------------------------+------------------------+---------------------------------+ -- another example: sa: |people list> => |Dan> + |Libby> + |Craig> + |Liz> + |Kathleen> + |Damian> + |Martin> sa: table[name,wife,where-live,lives-with,knows-quite-well] "" |people list> +----------+------+---------------------------+--------------+---------------------------+ | name | wife | where-live | lives-with | knows-quite-well | +----------+------+---------------------------+--------------+---------------------------+ | Dan | | UK: Bristol: Zetland road | Libby, Craig | | | Libby | | | | | | Craig | Liz | | | | | Liz | | UK: Bristol | Kathleen | | | Kathleen | | | | | | Damian | | UK: London | | | | Martin | | | | Craig, Damian, Dan, Libby | +----------+------+---------------------------+--------------+---------------------------+And I guess that is about it for this example. Though I guess we could again make the observation that even if we have no data on an operator applied to a ket, the code handles it gracefully.
Thursday, 29 January 2015
another pretty print table example
Recall some of the data from the other day. Well, let's pretty print some of that.
pretty print some data about Australian cities
So, in my travels trying to work out how to write the pretty print table code (and yeah, I wrote my code from scratch, rather than copying anyone else's code), I found this page. Now, I did not even look at the code used there, but I did borrow the data in his table. Let's pretty print that with my new code:
-- first some knowledge: sa: load pretty-print-table-of-australian-cities.sw sa: dump ---------------------------------------- |context> => |context: pretty print table of Australian cities> |city list> => |Adelaide> + |Brisbane> + |Darwin> + |Hobart> + |Melbourne> + |Perth> + |Sydney> area |Adelaide> => |1295> population |Adelaide> => |1158259> annual-rainfall |Adelaide> => |mm: 600.5> area |Brisbane> => |5905> population |Brisbane> => |1857594> annual-rainfall |Brisbane> => |mm: 1146.4> area |Darwin> => |112> population |Darwin> => |120900> annual-rainfall |Darwin> => |mm: 1714.7> area |Hobart> => |1357> population |Hobart> => |205556> annual-rainfall |Hobart> => |mm: 619.5> area |Melbourne> => |1566> population |Melbourne> => |3806092> annual-rainfall |Melbourne> => |mm: 646.9> area |Perth> => |5386> population |Perth> => |1554769> annual-rainfall |Perth> => |mm: 869.4> area |Sydney> => |2058> population |Sydney> => |4336374> annual-rainfall |Sydney> => |mm: 1214.8> ----------------------------------------Now, let's pretty print it:
sa: table[city-name,area,population,annual-rainfall] "" |city list> +-----------+------+------------+-----------------+ | city-name | area | population | annual-rainfall | +-----------+------+------------+-----------------+ | Adelaide | 1295 | 1158259 | mm: 600.5 | | Brisbane | 5905 | 1857594 | mm: 1146.4 | | Darwin | 112 | 120900 | mm: 1714.7 | | Hobart | 1357 | 205556 | mm: 619.5 | | Melbourne | 1566 | 3806092 | mm: 646.9 | | Perth | 5386 | 1554769 | mm: 869.4 | | Sydney | 2058 | 4336374 | mm: 1214.8 | +-----------+------+------------+-----------------+Cool and pretty! Heaps more to come!
new function: pretty print a table
Just as promised recently, we can add more functions when we think of a new need. Today, it took a while, but I wrote a pretty print table function. Feed it a superposition, apply a bunch of operators to it, then spit out a pretty table.
General usage:
table[first-column-heading,op1,op2,...] some-superposition
So, here are some examples. First up temperature:
Next, some general info about a couple of people. First load up in sw format:
mother |Fred> => |Jane>
father |Fred> => |Robert>
age |Fred> => |age: 21>
height |Fred> => |cm: 179>
mother |Sam> => |Betty>
father |Sam> => |Tom>
age |Sam> => |age: 27>
height |Sam> => |cm: 183>
mother |Nicole> => |Bev>
height |Nicole> => |cm: 168>
Next example, pretty printing some of what we know about early US presidents:
Update: an important thing to note is that these tables are not just of stored values. Some of the entries (eg, is-teenager, is-adult, years-in-office) are calculated at the time we generate the table. And they are again generated next time we ask the code to spit out a table. Remember, to generate our tables we are applying operators to the incoming superposition, not just looking up values. One consequence is that if in the background we update Emma's age (she had a birthday, perhaps, or we discovered we had made a mistake) the is-teenager and is-adult operators will do the right thing. No need to update those elements manually, as we would have to do if we were working with just stored values. Besides, if you do want to store values, instead of calculating over and over with each table, just use the map function. Perhaps I will explain later! Of course, if you do this, and then you change the definition of your operator, then the stored values will not be updated.
Another thing to note is that if you want a different name for your column heading than the operator name, just use the standard method for defining an alias. eg:
better-column-name |*> #=> unwanted-operator-name |_self>
And instead of:
table[foo,unwanted-operator-name] "" |list>
use:
table[foo,better-column-name] "" |list>
General usage:
table[first-column-heading,op1,op2,...] some-superposition
So, here are some examples. First up temperature:
-- NB: that due to quirks of the parser we need to do these two first:
-- (essentially casting function operators {F,K} to literal operators)
sa: F |*> #=> F |_self>
sa: K |*> #=> K |_self>
-- now, spit out a temperature table:
sa: table[C,F,K] range(|C: 0>,|C: 100>,|10>)
+--------+-----------+-----------+
| C | F | K |
+--------+-----------+-----------+
| C: 0 | F: 32.00 | K: 273.15 |
| C: 10 | F: 50.00 | K: 283.15 |
| C: 20 | F: 68.00 | K: 293.15 |
| C: 30 | F: 86.00 | K: 303.15 |
| C: 40 | F: 104.00 | K: 313.15 |
| C: 50 | F: 122.00 | K: 323.15 |
| C: 60 | F: 140.00 | K: 333.15 |
| C: 70 | F: 158.00 | K: 343.15 |
| C: 80 | F: 176.00 | K: 353.15 |
| C: 90 | F: 194.00 | K: 363.15 |
| C: 100 | F: 212.00 | K: 373.15 |
+--------+-----------+-----------+
Now, what is going on underneath? Well the first column is just the superposition we have fed in (and uses the first operator "C" as its column heading), then the next two columns are generated by applying the F and K literal operators to the incoming superposition.Next, some general info about a couple of people. First load up in sw format:
mother |Fred> => |Jane>
father |Fred> => |Robert>
age |Fred> => |age: 21>
height |Fred> => |cm: 179>
mother |Sam> => |Betty>
father |Sam> => |Tom>
age |Sam> => |age: 27>
height |Sam> => |cm: 183>
mother |Nicole> => |Bev>
height |Nicole> => |cm: 168>
-- Now pretty print as a table: sa: table[name,mother,father,age,height] (|Fred> + |Nicole> + |Sam>) +--------+--------+--------+---------+---------+ | name | mother | father | age | height | +--------+--------+--------+---------+---------+ | Fred | Jane | Robert | age: 21 | cm: 179 | | Nicole | Bev | | | cm: 168 | | Sam | Betty | Tom | age: 27 | cm: 183 | +--------+--------+--------+---------+---------+Noting that it gracefully handles not knowing something, in this table, Nicole's father and age.
Next example, pretty printing some of what we know about early US presidents:
sa: load early-us-presidents.sw sa: table[name,full-name,president-number,party] "" |early US Presidents: _list> +------------+---------------------------+------------------+------------------------------+ | name | full-name | president-number | party | +------------+---------------------------+------------------+------------------------------+ | Washington | person: George Washington | number: 1 | party: Independent | | Adams | person: John Adams | number: 2 | party: Federalist | | Jefferson | person: Thomas Jefferson | number: 3 | party: Democratic-Republican | | Madison | person: James Madison | number: 4 | party: Democratic-Republican | | Monroe | person: James Monroe | number: 5 | party: Democratic-Republican | | Q Adams | person: John Quincy Adams | number: 6 | party: Democratic-Republican | +------------+---------------------------+------------------+------------------------------+ sa: years-in-office |*> #=> extract-value president-era |_self> sa: table[name,years-in-office] "" |early US Presidents: _list> +------------+------------------------------------------------------+ | name | years-in-office | +------------+------------------------------------------------------+ | Washington | 1789, 1790, 1791, 1792, 1793, 1794, 1795, 1796, 1797 | | Adams | 1797, 1798, 1799, 1800, 1801 | | Jefferson | 1801, 1802, 1803, 1804, 1805, 1806, 1807, 1808, 1809 | | Madison | 1809, 1810, 1811, 1812, 1813, 1814, 1815, 1816, 1817 | | Monroe | 1817, 1818, 1819, 1820, 1821, 1822, 1823, 1824, 1825 | | Q Adams | 1825, 1826, 1827, 1828, 1829 | +------------+------------------------------------------------------+Now, another example that ties in with my recent post:
-- load up some knowledge: age |person: Emma> => |age: 12> age |person: Fred> => |age: 17> age |person: Sam> => |age: 18> age |person: Liz> => |age: 19> age |person: Jack> => |age: 20> is-teenager |person: *> #=> do-you-know drop-below[13] drop-above[19] pop-float age |_self> is-adult |person: *> #=> do-you-know drop-below[18] pop-float age|_self> |list> => |person: Emma> + |person: Fred> + |person: Sam> + |person: Liz> + |person: Jack> -- take a look in table format: sa: table[name,age,is-teenager,is-adult] "" |list> +--------------+---------+-------------+----------+ | name | age | is-teenager | is-adult | +--------------+---------+-------------+----------+ | person: Emma | age: 12 | no | no | | person: Fred | age: 17 | yes | no | | person: Sam | age: 18 | yes | yes | | person: Liz | age: 19 | yes | yes | | person: Jack | age: 20 | no | yes | +--------------+---------+-------------+----------+Now, an example that ties in with my example of a simple network:
-- load up the data: sa: load simple-network.sw -- define some operators: -- (and again, due to the parser, we have to do it indirectly) sa: O2 |*> #=> O^2 |_self> sa: O3 |*> #=> O^3 |_self> sa: O4 |*> #=> O^4 |_self> sa: O5 |*> #=> O^5 |_self> -- take a look: sa: table[position,O,O2,O3,O4,O5] relevant-kets[O] +----------+--------+--------+--------+--------+--------+ | position | O | O2 | O3 | O4 | O5 | +----------+--------+--------+--------+--------+--------+ | a1 | a2 | a3 | a4 | a5 | a6 | | a2 | a3 | a4 | a5 | a6 | a7 | | a3 | a4 | a5 | a6 | a7 | a8 | | a4 | a5 | a6 | a7 | a8 | a9 | | a5 | a6 | a7 | a8 | a9 | a10 | | a6 | a7 | a8 | a9 | a10 | a1, b1 | | a7 | a8 | a9 | a10 | a1, b1 | a2, b2 | | a8 | a9 | a10 | a1, b1 | a2, b2 | a3, b3 | | a9 | a10 | a1, b1 | a2, b2 | a3, b3 | a4, b4 | | a10 | a1, b1 | a2, b2 | a3, b3 | a4, b4 | a5, b5 | | b1 | b2 | b3 | b4 | b5 | b6 | | b2 | b3 | b4 | b5 | b6 | b7 | | b3 | b4 | b5 | b6 | b7 | b1 | | b4 | b5 | b6 | b7 | b1 | b2 | | b5 | b6 | b7 | b1 | b2 | b3 | | b6 | b7 | b1 | b2 | b3 | b4 | | b7 | b1 | b2 | b3 | b4 | b5 | +----------+--------+--------+--------+--------+--------+And I guess that is about it. This thing is going to be useful all over the place.
Update: an important thing to note is that these tables are not just of stored values. Some of the entries (eg, is-teenager, is-adult, years-in-office) are calculated at the time we generate the table. And they are again generated next time we ask the code to spit out a table. Remember, to generate our tables we are applying operators to the incoming superposition, not just looking up values. One consequence is that if in the background we update Emma's age (she had a birthday, perhaps, or we discovered we had made a mistake) the is-teenager and is-adult operators will do the right thing. No need to update those elements manually, as we would have to do if we were working with just stored values. Besides, if you do want to store values, instead of calculating over and over with each table, just use the map function. Perhaps I will explain later! Of course, if you do this, and then you change the definition of your operator, then the stored values will not be updated.
Another thing to note is that if you want a different name for your column heading than the operator name, just use the standard method for defining an alias. eg:
better-column-name |*> #=> unwanted-operator-name |_self>
And instead of:
table[foo,unwanted-operator-name] "" |list>
use:
table[foo,better-column-name] "" |list>
Tuesday, 27 January 2015
is-teenager and is-adult in BKO
OK. Here is a fun and short one. Let's encode "is-teenager" and "is-adult" in BKO.
If we had less than and greater than implemented, we could do it directly:
is-teenager |person: *> #=> |age: 13> <= age|_self> <= |age: 19>
is-adult |person: *> #=> age|_self> >= |age: 18>
Now, they are not currently implemented (but presumably will be one day), but we can still do it indirectly (as is often the case):
is-teenager |person: *> #=> do-you-know drop-below[13] drop-above[19] pop-float age |_self>
is-adult |person: *> #=> do-you-know drop-below[18] pop-float age|_self>
-- feed in some ages:
age |person: Emma> => |age: 12>
age |person: Fred> => |age: 17>
age |person: Sam> => |age: 18>
age |person: Liz> => |age: 19>
age |person: Jack> => |age: 20>
-- now test it:
sa: is-teenager |person: Emma>
|no>
sa: is-adult |person: Emma>
|no>
sa: is-teenager |person: Fred>
|yes>
sa: is-adult |person: Fred>
|no>
sa: is-teenager |person: Sam>
|yes>
sa: is-adult |person: Sam>
|yes>
sa: is-teenager |person: Liz>
|yes>
sa: is-adult |person: Liz>
|yes>
sa: is-teenager |person: Jack>
|no>
sa: is-adult |person: Jack>
|yes>
Simple and fun! Heaps more to come!
Update: as in the is-late example, we can use the in-range sigmoid for is-teenager too, instead of using drop-below and drop-above (and I think in-range is a tad easier to understand):
If we had less than and greater than implemented, we could do it directly:
is-teenager |person: *> #=> |age: 13> <= age|_self> <= |age: 19>
is-adult |person: *> #=> age|_self> >= |age: 18>
Now, they are not currently implemented (but presumably will be one day), but we can still do it indirectly (as is often the case):
is-teenager |person: *> #=> do-you-know drop-below[13] drop-above[19] pop-float age |_self>
is-adult |person: *> #=> do-you-know drop-below[18] pop-float age|_self>
-- feed in some ages:
age |person: Emma> => |age: 12>
age |person: Fred> => |age: 17>
age |person: Sam> => |age: 18>
age |person: Liz> => |age: 19>
age |person: Jack> => |age: 20>
-- now test it:
sa: is-teenager |person: Emma>
|no>
sa: is-adult |person: Emma>
|no>
sa: is-teenager |person: Fred>
|yes>
sa: is-adult |person: Fred>
|no>
sa: is-teenager |person: Sam>
|yes>
sa: is-adult |person: Sam>
|yes>
sa: is-teenager |person: Liz>
|yes>
sa: is-adult |person: Liz>
|yes>
sa: is-teenager |person: Jack>
|no>
sa: is-adult |person: Jack>
|yes>
Simple and fun! Heaps more to come!
Update: as in the is-late example, we can use the in-range sigmoid for is-teenager too, instead of using drop-below and drop-above (and I think in-range is a tad easier to understand):
is-teenager |person: *> #=> do-you-know drop sigmoid-in-range[13,19] pop-float age |_self>
Sunday, 25 January 2015
FOAF vs sw
So, I was doing a little reading about FOAF, as it has some overlap with what I am trying to do. Anyway, here is a quote from that page:
Here's an example, a fragment from the mostly-fictional FOAF database. First we list some facts, then describe how the FOAF system makes it possible to explore the Web learning such things.
Feeling in a minimalist word mood, here is how we would represent that knowledge in sw:
- Find me today's web page recommendations made by people who work for Medical organisations
- Find me recent publications by people I've co-authored documents with
- Show me critiques of this web page, and the home pages of the author of that critique
"Find me today's web page recommendations made by people who work for Medical organisations"
-- first, we need to know a list of "medical organisations":
|medical organisations: list> => |med org: 1> + |med org: 2> + ...
-- then we need to know the employees of each of these:
employees |med org: 1> => |person 1> + |person: 2> + ...
employees |meg org: 2> => |person: 7> + |person 8> + ...
... and so on.
-- then we need to know "todays web page recommendations" for all those people:
todays-web-page-recommendations |person 1> => |url: a> + |url: b> + ...
...
todays-web-page-recommendations |person 15> => |url: p> + |url: q> + ...
-- then finally, we can ask our question:
todays-web-page-recommendations employees "" |medical organisations: list>
And to prove that works, I did a small test example in the console:
-- load in some sample knowledge:
|med org: list> => |med org 1> + |med org 2>
employees |med org 1> => |person 1>
employees |med org 2> => |person 2>
web-recommendation |person 1> => |url: a> + |url: b>
web-recommendation |person 2> => |url: p> + |url: q> + |url: r>
-- ask our question in the console:
sa: web-recommendation employees "" |med org: list>
|url: a> + |url: b> + |url: p> + |url: q> + |url: r>
"Find me recent publications by people I've co-authored documents with"
-- learn who we have co-authored with:
people-co-authored-with |me> => |Rob> + |Jack> + |Frank>
-- learn their recent publications:
recent-publications |Rob> => |paper: a> + |paper: b>
recent-publications |Jack> => |paper: j>
recent-publications |Frank> => |paper: s> + |paper: t> + |paper: x> + |paper: y> + |paper: z>
-- ask in the console:
sa: recent-publications people-co-authored-with |me>
|paper: a> + |paper: b> + |paper: j> + |paper: s> + |paper: t> + |paper: x> + |paper: y> + |paper: z>
"Show me critiques of this web page, and the home pages of the author of that critique"
-- learn critiques list:
list-of-critiques |this web page> => |critique 1> + |critique 2>
-- learn authors of those:
author |critique 1> => |Liz>
author |critique 2> => |Ron>
-- learn their homepages:
homepage |Liz> => |url: http://liz.org>
homepage |Ron> => |url: http://ron.org>
-- ask in the console:
sa: homepage author list-of-critiques |this web page>
|url: http://liz.org> + |url: http://ron.org>
Final example:
One page might tell use that "daniel.brickley@bristol.ac.uk works-at http://ilrt.org/". Another might tell use that "http://ilrt.org/ based-in bristol". On this basis, RDF-aware tools could conclude that the person whose email address is daniel.brickley@bristol.ac.uk works for an organisation based in Bristol.
-- learn this knowledge
works-at |daniel.brickley@bristol.ac.uk> => |http://ilrt.org/>
based-in |http://ilrt.org/> => |Bristol>
-- ask in the console:
sa: based-in works-at |daniel.brickley@bristol.ac.uk>
|Bristol>
And that is it for today! I hope a) the examples make sense, and b) I have shown a little of the power of the whole BKO scheme. Heh, and we haven't even used any function operators, this was all literal operators, and a big dose of linearity of literal operators.
I guess a couple of observations. 1) imagine how much harder this would be to do if we used standard neural net matrices and vectors. I think my symbolic notation is much simpler to use. 2) notice how close the questions asked in the console are to English. Again, another win for my notation.
Update: now we have pretty print table code, we can do things like:
Here's an example, a fragment from the mostly-fictional FOAF database. First we list some facts, then describe how the FOAF system makes it possible to explore the Web learning such things.
Dan lives in Zetland road, Bristol, UK with Libby and Craig. Dan's email address is danbri@w3.org. Libby's email address is libby.miller@bris.ac.uk. Craig's is craig@netgates.co.uk. Dan and Libby work for an organisation called "ILRT" whose website is at http://ilrt.org/. Craig works for "Netgates", an organisation whose website is at http://www.netgates.co.uk/.
Craig's wife Liz lives in Bristol with Kathleen. Kathleen and Liz also
work at "Netgates". Damian lives in London. Martin knows Craig, Damian,
Dan and Libby quite well. Martin lives in Bristol and has an email
address of m.l.poulter@bristol.ac.uk. (etc...)
Feeling in a minimalist word mood, here is how we would represent that knowledge in sw:
where-live |Dan> => |UK: Bristol: Zetland road> lives-with |Dan> => |Libby> + |Craig> email |Dan> => |email: danbri@w3.org> works-for |Dan> => |organisation: ILRT> email |Libby> => |email: libby.miller@bris.ac.uk> works-for |Libby> => |organisation: ILRT> email |Craig> => |email: craig@netgates.co.uk> works-for |Craig> => |organisation: Netgates> wife |Craig> => |Liz> where-live |Liz> => |UK: Bristol> lives-with |Liz> => |Kathleen> works-for |Liz> => |organisation: Netgates> works-for |Kathleen> => |organisation: Netgates> website |organisation: ILRT> => |url: http://ilrt.org/> website |organisation: Netgates> => |url: http://www.netgates.co.uk/> where-live |Damian> => |UK: London> knows-quite-well |Martin> => |Craig> + |Damian> + |Dan> + |Libby> where-lives |Martin> => |UK: Bristol> email |Martin> => |email: m.l.poulter@bristol.ac.uk>Next example on that page:
- Find me today's web page recommendations made by people who work for Medical organisations
- Find me recent publications by people I've co-authored documents with
- Show me critiques of this web page, and the home pages of the author of that critique
"Find me today's web page recommendations made by people who work for Medical organisations"
-- first, we need to know a list of "medical organisations":
|medical organisations: list> => |med org: 1> + |med org: 2> + ...
-- then we need to know the employees of each of these:
employees |med org: 1> => |person 1> + |person: 2> + ...
employees |meg org: 2> => |person: 7> + |person 8> + ...
... and so on.
-- then we need to know "todays web page recommendations" for all those people:
todays-web-page-recommendations |person 1> => |url: a> + |url: b> + ...
...
todays-web-page-recommendations |person 15> => |url: p> + |url: q> + ...
-- then finally, we can ask our question:
todays-web-page-recommendations employees "" |medical organisations: list>
And to prove that works, I did a small test example in the console:
-- load in some sample knowledge:
|med org: list> => |med org 1> + |med org 2>
employees |med org 1> => |person 1>
employees |med org 2> => |person 2>
web-recommendation |person 1> => |url: a> + |url: b>
web-recommendation |person 2> => |url: p> + |url: q> + |url: r>
-- ask our question in the console:
sa: web-recommendation employees "" |med org: list>
|url: a> + |url: b> + |url: p> + |url: q> + |url: r>
"Find me recent publications by people I've co-authored documents with"
-- learn who we have co-authored with:
people-co-authored-with |me> => |Rob> + |Jack> + |Frank>
-- learn their recent publications:
recent-publications |Rob> => |paper: a> + |paper: b>
recent-publications |Jack> => |paper: j>
recent-publications |Frank> => |paper: s> + |paper: t> + |paper: x> + |paper: y> + |paper: z>
-- ask in the console:
sa: recent-publications people-co-authored-with |me>
|paper: a> + |paper: b> + |paper: j> + |paper: s> + |paper: t> + |paper: x> + |paper: y> + |paper: z>
"Show me critiques of this web page, and the home pages of the author of that critique"
-- learn critiques list:
list-of-critiques |this web page> => |critique 1> + |critique 2>
-- learn authors of those:
author |critique 1> => |Liz>
author |critique 2> => |Ron>
-- learn their homepages:
homepage |Liz> => |url: http://liz.org>
homepage |Ron> => |url: http://ron.org>
-- ask in the console:
sa: homepage author list-of-critiques |this web page>
|url: http://liz.org> + |url: http://ron.org>
Final example:
One page might tell use that "daniel.brickley@bristol.ac.uk works-at http://ilrt.org/". Another might tell use that "http://ilrt.org/ based-in bristol". On this basis, RDF-aware tools could conclude that the person whose email address is daniel.brickley@bristol.ac.uk works for an organisation based in Bristol.
-- learn this knowledge
works-at |daniel.brickley@bristol.ac.uk> => |http://ilrt.org/>
based-in |http://ilrt.org/> => |Bristol>
-- ask in the console:
sa: based-in works-at |daniel.brickley@bristol.ac.uk>
|Bristol>
And that is it for today! I hope a) the examples make sense, and b) I have shown a little of the power of the whole BKO scheme. Heh, and we haven't even used any function operators, this was all literal operators, and a big dose of linearity of literal operators.
I guess a couple of observations. 1) imagine how much harder this would be to do if we used standard neural net matrices and vectors. I think my symbolic notation is much simpler to use. 2) notice how close the questions asked in the console are to English. Again, another win for my notation.
Update: now we have pretty print table code, we can do things like:
sa: author-homepage |*> #=> homepage author |_self> sa: table[critique,author,author-homepage] list-of-critiques |this web page> +------------+--------+-----------------+ | critique | author | author-homepage | +------------+--------+-----------------+ | critique 1 | Liz | http://liz.org | | critique 2 | Ron | http://ron.org | +------------+--------+-----------------+
Saturday, 24 January 2015
a big collection of function operators
I have been putting this off, as it will be quite a bit of work. But now is the time to try and describe some of the more interesting function operators. There is a whole collection of them (a quick grep says about 150 of them) in this file. And unlike the functions built into ket/sp classes, the plan is to add as many of these as we want or need. Indeed, get other people to write them too (if I can get others interested in this project). Note that behind the scenes, once you have a new function you need to "wire it in" to the processor. This currently means adding an entry into the appropriate hash-table (a black art that, on first try, I frequently get wrong! Though the console debugging info on similar functions is often helpful.)
Preamble over, let's jump in.
-- the ket-length function:
ket-length |abcde> == |number: len(abcde)>
-- the apply-value function:
apply-value |a: b: n> == n |a: b: n> (if n is a float)
apply-value |a: b: n> == |a: b: n> (otherwise)
-- the extract category/data-type function:
extract-category |a> == |>
extract-category |a: b> == |a>
extract-category |a: b: c> == |a: b>
-- the extract value function (the opposite of extract-category):
extract-value |a> == |a>
extract-value |a: b> == |b>
extract-value |a: b: c> == |c>
-- the category depth function:
cat-depth |> == |number: 0>
cat-depth |a> == |number: 1>
cat-depth |a: b> == |number: 2>
cat-depth |a: b: c> == |number: 3>
cat-depth |a: b: c: d: e: f: g> == |number: 7>
-- the expand-hierarchy function:
sa: expand-hierarchy |a: b: c: d: e>
|a> + |a: b> + |a: b: c> + |a: b: c: d> + |a: b: c: d: e>
-- pop-float and push-float
-- Here are some examples:
-- NB: this is not |>, there is a space in there, an important distinction!
pop-float |3.2> == 3.2| >
pop-float 5|7> == 35| > -- NB: the multiplication of 5 and 7
pop-float |x: 2> == 2|x>
pop-float 5.1|x: y: 2> == 10.2|x: y> -- NB: the multiplication of 5.1 and 2
pop-float |x: y> == |x: y>
push-float n|> == |> for all n
push-float 3| > == |3> (NB: the space in there, | > not |>)
push-float |x> == |x: 1>
push-float 3|x> == |x: 3>
push-float 3.2|x: y > == |x: y: 3.2>
-- a couple of example usages:
-- action man reached a height 4 times that of everest
-- first, learn height of everest:
height |everest> => |km: 8>
-- learn height of "action man", noting that the units of height for everest are irrelevant.
height |action man> => push-float 4 pop-float height |everest>
-- "some mountain" is 1/3 the height of everest
height |some mountain> => push-float 0.3333 pop-float height |everest>
-- the to-coeff function
-- kind of a dual to the clean sigmoid
-- clean sets all coeffs to 1
-- to-coeff sets all labels to | >
-- (excluding the identity operator, which we leave intact)
to-coeff n|> == |> for all n
to-coeff n|a> == n| > for all a
-- the to-number function
-- eg, as used in the algebra() code
-- idea, is to map all types of kets to the form "n | >", where n is a float
to-number |7.2> == 7.200| >
to-number 3|9> == 27| >
to-number |number: 3.1415> == 3.142| >
to-number 8|number: 3> == 24.000| >
-- NB: this code treats the "number" data-type differently than other types:
to-number |number: not-a-float> == 0| >
-- when you use a data-type other than "number" we just return the input ket:
to-number |a: b> == |a: b>
to-number 27|a: b: c: d: e> == 27.000|a: b: c: d: e>
-- the round[t] function
-- rounds floats to t decimal places
-- round[t] |a: b: n> == |a: b: round(n,t)> if n is a float, else |a: b: n>
-- eg:
round[2] |pi: 3.14159265> == |pi: 3.14>
round[7] |a: b: c> == |a: b: c>
-- the range function (this one is very useful in defining lists to work on):
-- categories/data-types must be equal:
-- in this case "a" != "b"
sa: range(|a: 2>,|b: 5>)
|>
-- default is step of size 1
sa: range(|5>,|11>)
|5> + |6> + |7> + |8> + |9> + |10> + |11>
-- specify a data-type (here "x"):
sa: range(|x: 1>,|x: 6>)
|x: 1> + |x: 2> + |x: 3> + |x: 4> + |x: 5> + |x: 6>
-- step size of 2
sa: range(|5>,|11>,|2>)
|5> + |7> + |9> + |11>
-- float step size of 0.25
sa: range(|5>,|7>,|0.25>)
|5.00> + |5.25> + |5.50> + |5.75> + |6.00> + |6.25> + |6.50> + |6.75> + |7.00>
-- negative step sizes is currently broken!
range(|5>,|8>,|-1>) == |>
range(|8>,|5>,|-1>) == |8> + |7>
-- the arithmetic function:
-- categories/data-types must be equal (to prevent mix type errors):
-- in this case "a" != "b"
arithmetic(|a: 5>,|+>,|b: 3>) == |>
-- this is one way to ensure data-types are equal:
-- NB: the to-km operator applied to the ket using miles.
arithmetic(to-km |miles: 5>,|+>,|km: 3>) == |km: 11.047>
-- more generally (assuming "a" and "b" have to-X defined correctly):
arithmetic(to-X |a>,|op>,to-X |b>)
Final note, arithmetic supports these operators: +, -, *, /, %, ^
(addition, subtraction, multiplication, division, modulus, exponentiation)
-- the algebra function:
-- (13x + 17)*(19y + 2z + 5)
sa: algebra(13|x> + |17>,|*>,19|y> + 2|z> + |5>)
247.000|x*y> + 26.000|x*z> + 65.000|x> + 323.000|y> + 34.000|z> + 85.000| >
-- (a + b)^6
sa: algebra(|a> + |b>,|^>,|6>)
|a*a*a*a*a*a> + 6.000|a*a*a*a*a*b> + 15.000|a*a*a*a*b*b> + 20.000|a*a*a*b*b*b> + 15.000|a*a*b*b*b*b> + 6.000|a*b*b*b*b*b> + |b*b*b*b*b*b>
And note that algebra currently supports these operators: +, -, *, ^
(addition, subtraction, multiplication, exponentiation)
Also note that currently algebra is Abelian,
ie, labels commute: |x*y> == |y*x>
-- set union and intersection:
-- if coeffs are in {0,1} it works like standard union and intersection:
sa: union(|a> + |c> + |d>,|a> + |b> + |c> + |d> + |e>)
|a> + |c> + |d> + |b> + |e>
sa: intersection(|a> + |c> + |d>,|a> + |b> + |c> + |d> + |e>)
|a> + |c> + |d>
-- if coeffs are not strictly {0,1} then union is max(a,b) and intersection is min(a,b)
-- eg, the simplest possible example:
sa: union(3|a>,7|a>)
7.000|a>
sa: intersection(3|a>,7|a>)
3.000|a>
-- extends in the obvious way for more interesting superpositions:
sa: union(2|a> + 0.3|b> + 0|c> + 13|d> + 0.9|e>,|a> + 11|b> + 23|c> + 0.5|d> + 7|e>)
2.000|a> + 11.000|b> + 23.000|c> + 13.000|d> + 7.000|e>
sa: intersection(2|a> + 0.3|b> + 0|c> + 13|d> + 0.9|e>,|a> + 11|b> + 23|c> + 0.5|d> + 7|e>)
|a> + 0.300|b> + 0.500|d> + 0.900|e>
-- using the same back-end code, we can implement other examples of foo(a,b).
-- eg, multiplication and addition, and so on.
sa: multiply(2|a> + 3|b> + 5|c>,7|a> + 5|b> + 0|c> + 9|d>)
14.000|a> + 15.000|b> + 0.000|c> + 0.000|d>
sa: addition(2|a> + 3|b> + 5|c>,7|a> + 5|b> + 0|c> + 9|d>)
9.000|a> + 8.000|b> + 5.000|c> + 9.000|d>
-- now a couple of really simple ones:
-- spell and read:
sa: spell |word: frog>
|letter: f> + |letter: r> + |letter: o> + |letter: g>
-- NB: since it is a superposition, the duplicate letters get added together.
-- plan is to eventually have a sequence type, where this doesn't happen
-- in that case we would instead have:
-- |letter: l> . |letter: e> . |letter: t> . |letter: t> . |letter: e> . |letter: r>
sa: spell |word: letter>
|letter: l> + 2.000|letter: e> + 2.000|letter: t> + |letter: r>
-- NB: read ignores case and punctuation, as we can see:
sa: read |text: I don't know about that!>
|word: i> + |word: don't> + |word: know> + |word: about> + |word: that>
-- now, spell assumes the "word" data-type, and read assumes the "text" data-type
-- and returns |> if they are not, but if it turns out this isn't useful (I think it will be),
-- it is trivial to change.
-- now, their inverse, which I had totally forgotten about (heh, that's how useful they are :).
sa: read-letters spell |word: letter>
|word: letter>
sa: read-words read |text: I don't know about that!>
|text: i don't know about that>
-- again, they would work better using sequences, not superpositions.
-- now code wise simple, but useful:
-- merge-labels()
sa: merge-labels(|a> + |b> + |c> + |d> + |e>)
|abcde>
-- now a couple of simple number related functions:
is-prime |number: n> == |yes> (if n is prime)
is-prime |number: n> == |no> (if n is not prime)
is-prime |blah> == |> (since we require the "number" data-type)
is-prime |blah: n> == |>
factor |number: n> returns list of prime factors, and again requires the "number" data-type.
sa: is-prime |number: 21>
|no>
-- as far as I know the python is using arbitrary precision integers:
sa: is-prime |number: 90214539181246357>
|yes>
sa: factor |number: 210>
|number: 2> + |number: 3> + |number: 5> + |number: 7>
sa: factor |number: 398714527>
|number: 521> + |number: 765287>
sa: factor |number: 987298762329>
4.000|number: 3> + |number: 11> + |number: 1108079419>
-- convert numbers into the word equivalent
-- (and eventually we would want the inverse too)
-- currently unimplemented!
-- though it would look something like this:
number-to-words |number: 7> => |text: seven>
number-to-words |number: 35> => |text: thirty five>
number-to-words |number: 137> => |text: one hundred and thirty seven>
number-to-words |number: 8,921> => |text: eight thousand, nine hundred and twenty one>
number-to-words |number: 54,329> => |text: fifty four thousand, three hundred and twenty nine>
number-to-words |number: 673,421> => |text: six hundred and seventy three thousand, four hundred and twenty one>
number-to-words |number: 3,896,520> => |text: three million, eight hundred and ninety six thousand, five hundred and twenty>
-- convert decimal number to another base:
sa: to-base(|350024>,|2>)
0.000|1> + 0.000|2> + 0.000|4> + |8> + 0.000|16> + 0.000|32> + |64> + 0.000|128> + |256> + |512> + |1024> + 0.000|2048> + |4096> + 0.000|8192> + |16384> + 0.000|32768> + |65536> + 0.000|131072> + |262144>
sa: to-base(|350024>,|8>)
0.000|1> + |8> + 5.000|64> + 3.000|512> + 5.000|4096> + 2.000|32768> + |262144>
sa: to-base(|350024>,|10>)
4.000|1> + 2.000|10> + 0.000|100> + 0.000|1000> + 5.000|10000> + 3.000|100000>
-- now a couple of functions to swap between temperature and distance units
-- proof of concept really, in practice we would want more (for other unit types),
-- and a cleaner way to implement them
-- F operator maps Celcius and Kelvin to Fahrenheit:
sa: F |C: 0>
|F: 32.00>
sa: F |C: 100>
|F: 212.00>
sa: F |K: 0>
|F: -459.67>
-- C maps Fahrenheit and Kelvin to Celcius:
sa: C |K: 0>
|C: -273.15>
sa: C |F: 0>
|C: -17.78>
sa: C |F: 100>
|C: 37.78>
-- K maps Fahrenheit and Celcius to Kelvin:
sa: K |C: 18>
|K: 291.15>
sa: K |C: 0>
|K: 273.15>
sa: K |F: 100>
|K: 310.93>
-- now similar, but for distances:
-- to-km maps meters or miles to km:
sa: to-km |miles: 1>
|km: 1.609>
-- to-meter maps km or miles to meters
sa: to-meter |miles: 7>
|m: 11265.408>
sa: to-meter |km: 5.213>
|m: 5213.000>
-- to-mile(s) maps km or m to miles
sa: to-miles |km: 42>
|miles: 26.098>
sa: to-miles |m: 800>
|miles: 0.497>
-- now a fun one! This should be useful in a bunch of places:
-- the list-to-words function:
list-to-words |x> == |x>
list-to-words (|x> + |y>) == |x and y>
list-to-words (|x> + |y> + |z>) == |x, y and z>
list-to-words (|x> + |y> + |z> + |u> + |v>) == |x, y, z, u and v>
and so on.
-- a practical example:
-- learn Eric's list of friends:
sa: friends |person: Eric> => |person: Fred> + |person: Sam> + |person: Harry> + |person: Mary> + |person: liz>
-- output Eric's list of friends:
sa: list-to-words extract-value friends |person: Eric>
|Fred, Sam, Harry, Mary and liz>
-- the "common" function (a type of intersection)
-- (though intersection is currently limited to 2 or 3 parameters, common can handle any number)
common[op] (|x> + |y> + |z>)
-- expands to:
intersection(op|x>, op|y>, op|z>)
-- some common usages:
common[friends] (|Fred> + |Sam>)
common[actors] (|movie-1> + |movie-2>)
-- or indirectly:
|list> => |Fred> + |Sam> + |Charles> + |Liz>
common[friends] "" |list>
-- next, we have an if statement in BKO.
-- really does require its' own post, to explain best how to use it. Perhaps later.
-- raw details are just:
if(|x>,|a>,|b>) returns |a> if |x> == |True>, |b> otherwise
-- and its more useful brother (since we try to avoid just living in the {0,1} world):
-- the weighted-if function:
wif(|x>,|a>,|b>)
eg:
wif(0.7|x>,|a>,|b>)
if |x> == |True>, returns 0.7|a> + 0.3|b>
if |x> != |True>, returns 0.3|a> + 0.7|b>
-- next, the map function, again this one is very useful!
-- we need this since we don't have multi-line for loops, so we use this to map operators to a list of kets.
map[op] (|x> + |y> + |z>)
runs:
op |x> => op |_self>
op |y> => op |_self>
op |z> => op |_self>
map[fn,result] (|a> + |b> + |c> + |d>)
runs:
result |a> => fn |_self>
result |b> => fn |_self>
result |c> => fn |_self>
result |d> => fn |_self>
-- most common usage is:
fn |*> #=> ... some details here
map[fn,result] "" |some list>
-- the exp function:
exp[op,n] |x>
maps to:
(1 + op + op^2 + ... + op^n) |x>
-- the exp-max function:
exp-max[op] |x>
maps to:
(1 + op + op^2 + ... + op^n) |x>
for an n such that exp[op,n] |x> == exp[op,n+1] |x>
-- ie, we have found every "child node" of |x>
-- with a warning that we have no idea how big the result is going to be, or how many steps deep.
-- a common usage is to find 6 degrees of separation:
exp[friends,6] |Fred>
exp-max[friends] |Fred>
-- the apply() function:
-- again, this is one of those very useful ones!
eg: apply(|op: age> + |op: friends> + |op: father>,|Fred>)
maps to:
age |Fred> + friends |Fred> + father |Fred>
-- a common usage is to define a list of operators separately:
|op list> => |op: mother> + |op: father> + |op: dob> + |op: age>
-- then apply them:
apply("" |op list>,|Fred>)
-- eg, maybe use like this:
|basic info op list> => |op: mother> + |op: father> + |op: height> + |op: age> + |op: eye-colour>
basic-info |*> #=> apply("" |basic info op list>,|_self>)
basic-info |Fred>
basic-info |Sam>
-- here is a toy function, maps dates to day of the week:
sa: day-of-the-week |date: 2015/01/24>
|day: Saturday>
-- here is one that saves typing, the split operator:
sa: split |a b c d e>
|a> + |b> + |c> + |d> + |e>
sa: split |word1 word2 word3 word4>
|word1> + |word2> + |word3> + |word4>
-- currently only splits on space chars, but maybe useful to specify the split char(s).
-- the clone ket function (not yet sure of a use case):
-- clone(|x>,|y>) copies rules from |x> and applies them to |y>
-- hence the name, clone().
-- say we have:
-- age |x> => |27>
-- mother |x> => |Jane>
-- after clone(|x>,|y>) we have:
-- age |y> == |27>
-- mother |y> == |Jane>
-- eg, if |x> and |y> are twin sisters.
--
-- thought of a use case:
-- say we have just learnt "elm" is a type of tree.
-- well, load that up with some default values we know about all tree's:
-- (cf. inheriting from a parent class in OO programming)
-- clone(|plant: tree>,|plant: tree: elm>)
-- then fill in more specific data as we learn more.
-- the relevant-kets[op] function
-- returns a list of all the kets in the current context that have "op" defined.
-- relevant-kets[op] is frequently useful for generating lists we can apply the map function to.
-- eg, learn some data:
sa: friends |Fred> => |Sam> + |Liz>
sa: friends |Rob> => |Jack> + |Tom>
sa: age |Fred> => |22>
-- now find who knows what operator types:
sa: relevant-kets[friends] |>
|Fred> + |Rob>
sa: relevant-kets[age] |>
|Fred>
-- there is a variant on this.
-- returns: intersection(relevant-kets[op],SP)
intn-relevant-kets[op] SP
-- eg, we can chain them and find all kets that support both friends, and age:
-- (NB: one has "intn" prefix, and one doesn't!)
intn-relevant-kets[age] relevant-kets[friends] |>
-- the pretty print rules as a matrix function.
-- first define some rules:
sa: op |a> => |a> + 2.000|b> + 3.000|c>
sa: op |b> => 0.500|b> + 9.000|c> + 5.000|e>
sa: op |c> => 7.000|e> + 2.000|b>
-- now take a look:
-- and we finish with a slightly more interesting function, the train-of-thought function.
-- this code makes heavy use of supported-ops, pick-elt and apply().
-- and will work much better with a big knowledge base, but even a small one gives hints of what a large example will be like.
sa: load early-us-presidents.sw -- load up some knowledge
sa: create inverse -- needed, else we run into dead ends.
sa: train-of-thought[13] |Madison> -- take 13 steps, starting with |Madison>
context: sw console
one: |Madison>
n: 13
|X>: |Madison>
|early US Presidents: _list>
|Adams>
|year: 1797>
|Washington>
|early US Presidents: _list>
|Adams>
|number: 2>
|Adams>
|year: 1801>
|Jefferson>
|early US Presidents: _list>
|Adams>
|year: 1799>
Anyway, I guess the summary of this post is that we have some proof of concept functions trying to map our BKO scheme towards a more general purpose knowledge engine. Don't take the above functions as finished, take them as hints on where we could take this project.
Preamble over, let's jump in.
-- the ket-length function:
ket-length |abcde> == |number: len(abcde)>
-- the apply-value function:
apply-value |a: b: n> == n |a: b: n> (if n is a float)
apply-value |a: b: n> == |a: b: n> (otherwise)
-- the extract category/data-type function:
extract-category |a> == |>
extract-category |a: b> == |a>
extract-category |a: b: c> == |a: b>
-- the extract value function (the opposite of extract-category):
extract-value |a> == |a>
extract-value |a: b> == |b>
extract-value |a: b: c> == |c>
-- the category depth function:
cat-depth |> == |number: 0>
cat-depth |a> == |number: 1>
cat-depth |a: b> == |number: 2>
cat-depth |a: b: c> == |number: 3>
cat-depth |a: b: c: d: e: f: g> == |number: 7>
-- the expand-hierarchy function:
sa: expand-hierarchy |a: b: c: d: e>
|a> + |a: b> + |a: b: c> + |a: b: c: d> + |a: b: c: d: e>
-- pop-float and push-float
-- Here are some examples:
-- NB: this is not |>, there is a space in there, an important distinction!
pop-float |3.2> == 3.2| >
pop-float 5|7> == 35| > -- NB: the multiplication of 5 and 7
pop-float |x: 2> == 2|x>
pop-float 5.1|x: y: 2> == 10.2|x: y> -- NB: the multiplication of 5.1 and 2
pop-float |x: y> == |x: y>
push-float n|> == |> for all n
push-float 3| > == |3> (NB: the space in there, | > not |>)
push-float |x> == |x: 1>
push-float 3|x> == |x: 3>
push-float 3.2|x: y > == |x: y: 3.2>
-- a couple of example usages:
-- action man reached a height 4 times that of everest
-- first, learn height of everest:
height |everest> => |km: 8>
-- learn height of "action man", noting that the units of height for everest are irrelevant.
height |action man> => push-float 4 pop-float height |everest>
-- "some mountain" is 1/3 the height of everest
height |some mountain> => push-float 0.3333 pop-float height |everest>
-- the to-coeff function
-- kind of a dual to the clean sigmoid
-- clean sets all coeffs to 1
-- to-coeff sets all labels to | >
-- (excluding the identity operator, which we leave intact)
to-coeff n|> == |> for all n
to-coeff n|a> == n| > for all a
-- the to-number function
-- eg, as used in the algebra() code
-- idea, is to map all types of kets to the form "n | >", where n is a float
to-number |7.2> == 7.200| >
to-number 3|9> == 27| >
to-number |number: 3.1415> == 3.142| >
to-number 8|number: 3> == 24.000| >
-- NB: this code treats the "number" data-type differently than other types:
to-number |number: not-a-float> == 0| >
-- when you use a data-type other than "number" we just return the input ket:
to-number |a: b> == |a: b>
to-number 27|a: b: c: d: e> == 27.000|a: b: c: d: e>
-- the round[t] function
-- rounds floats to t decimal places
-- round[t] |a: b: n> == |a: b: round(n,t)> if n is a float, else |a: b: n>
-- eg:
round[2] |pi: 3.14159265> == |pi: 3.14>
round[7] |a: b: c> == |a: b: c>
-- the range function (this one is very useful in defining lists to work on):
-- categories/data-types must be equal:
-- in this case "a" != "b"
sa: range(|a: 2>,|b: 5>)
|>
-- default is step of size 1
sa: range(|5>,|11>)
|5> + |6> + |7> + |8> + |9> + |10> + |11>
-- specify a data-type (here "x"):
sa: range(|x: 1>,|x: 6>)
|x: 1> + |x: 2> + |x: 3> + |x: 4> + |x: 5> + |x: 6>
-- step size of 2
sa: range(|5>,|11>,|2>)
|5> + |7> + |9> + |11>
-- float step size of 0.25
sa: range(|5>,|7>,|0.25>)
|5.00> + |5.25> + |5.50> + |5.75> + |6.00> + |6.25> + |6.50> + |6.75> + |7.00>
-- negative step sizes is currently broken!
range(|5>,|8>,|-1>) == |>
range(|8>,|5>,|-1>) == |8> + |7>
-- the arithmetic function:
-- categories/data-types must be equal (to prevent mix type errors):
-- in this case "a" != "b"
arithmetic(|a: 5>,|+>,|b: 3>) == |>
-- this is one way to ensure data-types are equal:
-- NB: the to-km operator applied to the ket using miles.
arithmetic(to-km |miles: 5>,|+>,|km: 3>) == |km: 11.047>
-- more generally (assuming "a" and "b" have to-X defined correctly):
arithmetic(to-X |a>,|op>,to-X |b>)
Final note, arithmetic supports these operators: +, -, *, /, %, ^
(addition, subtraction, multiplication, division, modulus, exponentiation)
-- the algebra function:
-- (13x + 17)*(19y + 2z + 5)
sa: algebra(13|x> + |17>,|*>,19|y> + 2|z> + |5>)
247.000|x*y> + 26.000|x*z> + 65.000|x> + 323.000|y> + 34.000|z> + 85.000| >
-- (a + b)^6
sa: algebra(|a> + |b>,|^>,|6>)
|a*a*a*a*a*a> + 6.000|a*a*a*a*a*b> + 15.000|a*a*a*a*b*b> + 20.000|a*a*a*b*b*b> + 15.000|a*a*b*b*b*b> + 6.000|a*b*b*b*b*b> + |b*b*b*b*b*b>
And note that algebra currently supports these operators: +, -, *, ^
(addition, subtraction, multiplication, exponentiation)
Also note that currently algebra is Abelian,
ie, labels commute: |x*y> == |y*x>
-- set union and intersection:
-- if coeffs are in {0,1} it works like standard union and intersection:
sa: union(|a> + |c> + |d>,|a> + |b> + |c> + |d> + |e>)
|a> + |c> + |d> + |b> + |e>
sa: intersection(|a> + |c> + |d>,|a> + |b> + |c> + |d> + |e>)
|a> + |c> + |d>
-- if coeffs are not strictly {0,1} then union is max(a,b) and intersection is min(a,b)
-- eg, the simplest possible example:
sa: union(3|a>,7|a>)
7.000|a>
sa: intersection(3|a>,7|a>)
3.000|a>
-- extends in the obvious way for more interesting superpositions:
sa: union(2|a> + 0.3|b> + 0|c> + 13|d> + 0.9|e>,|a> + 11|b> + 23|c> + 0.5|d> + 7|e>)
2.000|a> + 11.000|b> + 23.000|c> + 13.000|d> + 7.000|e>
sa: intersection(2|a> + 0.3|b> + 0|c> + 13|d> + 0.9|e>,|a> + 11|b> + 23|c> + 0.5|d> + 7|e>)
|a> + 0.300|b> + 0.500|d> + 0.900|e>
-- using the same back-end code, we can implement other examples of foo(a,b).
-- eg, multiplication and addition, and so on.
sa: multiply(2|a> + 3|b> + 5|c>,7|a> + 5|b> + 0|c> + 9|d>)
14.000|a> + 15.000|b> + 0.000|c> + 0.000|d>
sa: addition(2|a> + 3|b> + 5|c>,7|a> + 5|b> + 0|c> + 9|d>)
9.000|a> + 8.000|b> + 5.000|c> + 9.000|d>
-- now a couple of really simple ones:
-- spell and read:
sa: spell |word: frog>
|letter: f> + |letter: r> + |letter: o> + |letter: g>
-- NB: since it is a superposition, the duplicate letters get added together.
-- plan is to eventually have a sequence type, where this doesn't happen
-- in that case we would instead have:
-- |letter: l> . |letter: e> . |letter: t> . |letter: t> . |letter: e> . |letter: r>
sa: spell |word: letter>
|letter: l> + 2.000|letter: e> + 2.000|letter: t> + |letter: r>
-- NB: read ignores case and punctuation, as we can see:
sa: read |text: I don't know about that!>
|word: i> + |word: don't> + |word: know> + |word: about> + |word: that>
-- now, spell assumes the "word" data-type, and read assumes the "text" data-type
-- and returns |> if they are not, but if it turns out this isn't useful (I think it will be),
-- it is trivial to change.
-- now, their inverse, which I had totally forgotten about (heh, that's how useful they are :).
sa: read-letters spell |word: letter>
|word: letter>
sa: read-words read |text: I don't know about that!>
|text: i don't know about that>
-- again, they would work better using sequences, not superpositions.
-- now code wise simple, but useful:
-- merge-labels()
sa: merge-labels(|a> + |b> + |c> + |d> + |e>)
|abcde>
-- now a couple of simple number related functions:
is-prime |number: n> == |yes> (if n is prime)
is-prime |number: n> == |no> (if n is not prime)
is-prime |blah> == |> (since we require the "number" data-type)
is-prime |blah: n> == |>
factor |number: n> returns list of prime factors, and again requires the "number" data-type.
sa: is-prime |number: 21>
|no>
-- as far as I know the python is using arbitrary precision integers:
sa: is-prime |number: 90214539181246357>
|yes>
sa: factor |number: 210>
|number: 2> + |number: 3> + |number: 5> + |number: 7>
sa: factor |number: 398714527>
|number: 521> + |number: 765287>
sa: factor |number: 987298762329>
4.000|number: 3> + |number: 11> + |number: 1108079419>
-- convert numbers into the word equivalent
-- (and eventually we would want the inverse too)
-- currently unimplemented!
-- though it would look something like this:
number-to-words |number: 7> => |text: seven>
number-to-words |number: 35> => |text: thirty five>
number-to-words |number: 137> => |text: one hundred and thirty seven>
number-to-words |number: 8,921> => |text: eight thousand, nine hundred and twenty one>
number-to-words |number: 54,329> => |text: fifty four thousand, three hundred and twenty nine>
number-to-words |number: 673,421> => |text: six hundred and seventy three thousand, four hundred and twenty one>
number-to-words |number: 3,896,520> => |text: three million, eight hundred and ninety six thousand, five hundred and twenty>
-- convert decimal number to another base:
sa: to-base(|350024>,|2>)
0.000|1> + 0.000|2> + 0.000|4> + |8> + 0.000|16> + 0.000|32> + |64> + 0.000|128> + |256> + |512> + |1024> + 0.000|2048> + |4096> + 0.000|8192> + |16384> + 0.000|32768> + |65536> + 0.000|131072> + |262144>
sa: to-base(|350024>,|8>)
0.000|1> + |8> + 5.000|64> + 3.000|512> + 5.000|4096> + 2.000|32768> + |262144>
sa: to-base(|350024>,|10>)
4.000|1> + 2.000|10> + 0.000|100> + 0.000|1000> + 5.000|10000> + 3.000|100000>
-- now a couple of functions to swap between temperature and distance units
-- proof of concept really, in practice we would want more (for other unit types),
-- and a cleaner way to implement them
-- F operator maps Celcius and Kelvin to Fahrenheit:
sa: F |C: 0>
|F: 32.00>
sa: F |C: 100>
|F: 212.00>
sa: F |K: 0>
|F: -459.67>
-- C maps Fahrenheit and Kelvin to Celcius:
sa: C |K: 0>
|C: -273.15>
sa: C |F: 0>
|C: -17.78>
sa: C |F: 100>
|C: 37.78>
-- K maps Fahrenheit and Celcius to Kelvin:
sa: K |C: 18>
|K: 291.15>
sa: K |C: 0>
|K: 273.15>
sa: K |F: 100>
|K: 310.93>
-- now similar, but for distances:
-- to-km maps meters or miles to km:
sa: to-km |miles: 1>
|km: 1.609>
-- to-meter maps km or miles to meters
sa: to-meter |miles: 7>
|m: 11265.408>
sa: to-meter |km: 5.213>
|m: 5213.000>
-- to-mile(s) maps km or m to miles
sa: to-miles |km: 42>
|miles: 26.098>
sa: to-miles |m: 800>
|miles: 0.497>
-- now a fun one! This should be useful in a bunch of places:
-- the list-to-words function:
list-to-words |x> == |x>
list-to-words (|x> + |y>) == |x and y>
list-to-words (|x> + |y> + |z>) == |x, y and z>
list-to-words (|x> + |y> + |z> + |u> + |v>) == |x, y, z, u and v>
and so on.
-- a practical example:
-- learn Eric's list of friends:
sa: friends |person: Eric> => |person: Fred> + |person: Sam> + |person: Harry> + |person: Mary> + |person: liz>
-- output Eric's list of friends:
sa: list-to-words extract-value friends |person: Eric>
|Fred, Sam, Harry, Mary and liz>
-- the "common" function (a type of intersection)
-- (though intersection is currently limited to 2 or 3 parameters, common can handle any number)
common[op] (|x> + |y> + |z>)
-- expands to:
intersection(op|x>, op|y>, op|z>)
-- some common usages:
common[friends] (|Fred> + |Sam>)
common[actors] (|movie-1> + |movie-2>)
-- or indirectly:
|list> => |Fred> + |Sam> + |Charles> + |Liz>
common[friends] "" |list>
-- next, we have an if statement in BKO.
-- really does require its' own post, to explain best how to use it. Perhaps later.
-- raw details are just:
if(|x>,|a>,|b>) returns |a> if |x> == |True>, |b> otherwise
-- and its more useful brother (since we try to avoid just living in the {0,1} world):
-- the weighted-if function:
wif(|x>,|a>,|b>)
eg:
wif(0.7|x>,|a>,|b>)
if |x> == |True>, returns 0.7|a> + 0.3|b>
if |x> != |True>, returns 0.3|a> + 0.7|b>
-- next, the map function, again this one is very useful!
-- we need this since we don't have multi-line for loops, so we use this to map operators to a list of kets.
map[op] (|x> + |y> + |z>)
runs:
op |x> => op |_self>
op |y> => op |_self>
op |z> => op |_self>
map[fn,result] (|a> + |b> + |c> + |d>)
runs:
result |a> => fn |_self>
result |b> => fn |_self>
result |c> => fn |_self>
result |d> => fn |_self>
-- most common usage is:
fn |*> #=> ... some details here
map[fn,result] "" |some list>
-- the exp function:
exp[op,n] |x>
maps to:
(1 + op + op^2 + ... + op^n) |x>
-- the exp-max function:
exp-max[op] |x>
maps to:
(1 + op + op^2 + ... + op^n) |x>
for an n such that exp[op,n] |x> == exp[op,n+1] |x>
-- ie, we have found every "child node" of |x>
-- with a warning that we have no idea how big the result is going to be, or how many steps deep.
-- a common usage is to find 6 degrees of separation:
exp[friends,6] |Fred>
exp-max[friends] |Fred>
-- the apply() function:
-- again, this is one of those very useful ones!
eg: apply(|op: age> + |op: friends> + |op: father>,|Fred>)
maps to:
age |Fred> + friends |Fred> + father |Fred>
-- a common usage is to define a list of operators separately:
|op list> => |op: mother> + |op: father> + |op: dob> + |op: age>
-- then apply them:
apply("" |op list>,|Fred>)
-- eg, maybe use like this:
|basic info op list> => |op: mother> + |op: father> + |op: height> + |op: age> + |op: eye-colour>
basic-info |*> #=> apply("" |basic info op list>,|_self>)
basic-info |Fred>
basic-info |Sam>
-- here is a toy function, maps dates to day of the week:
sa: day-of-the-week |date: 2015/01/24>
|day: Saturday>
-- here is one that saves typing, the split operator:
sa: split |a b c d e>
|a> + |b> + |c> + |d> + |e>
sa: split |word1 word2 word3 word4>
|word1> + |word2> + |word3> + |word4>
-- currently only splits on space chars, but maybe useful to specify the split char(s).
-- the clone ket function (not yet sure of a use case):
-- clone(|x>,|y>) copies rules from |x> and applies them to |y>
-- hence the name, clone().
-- say we have:
-- age |x> => |27>
-- mother |x> => |Jane>
-- after clone(|x>,|y>) we have:
-- age |y> == |27>
-- mother |y> == |Jane>
-- eg, if |x> and |y> are twin sisters.
--
-- thought of a use case:
-- say we have just learnt "elm" is a type of tree.
-- well, load that up with some default values we know about all tree's:
-- (cf. inheriting from a parent class in OO programming)
-- clone(|plant: tree>,|plant: tree: elm>)
-- then fill in more specific data as we learn more.
-- the relevant-kets[op] function
-- returns a list of all the kets in the current context that have "op" defined.
-- relevant-kets[op] is frequently useful for generating lists we can apply the map function to.
-- eg, learn some data:
sa: friends |Fred> => |Sam> + |Liz>
sa: friends |Rob> => |Jack> + |Tom>
sa: age |Fred> => |22>
-- now find who knows what operator types:
sa: relevant-kets[friends] |>
|Fred> + |Rob>
sa: relevant-kets[age] |>
|Fred>
-- there is a variant on this.
-- returns: intersection(relevant-kets[op],SP)
intn-relevant-kets[op] SP
-- eg, we can chain them and find all kets that support both friends, and age:
-- (NB: one has "intn" prefix, and one doesn't!)
intn-relevant-kets[age] relevant-kets[friends] |>
-- the pretty print rules as a matrix function.
-- first define some rules:
sa: op |a> => |a> + 2.000|b> + 3.000|c>
sa: op |b> => 0.500|b> + 9.000|c> + 5.000|e>
sa: op |c> => 7.000|e> + 2.000|b>
-- now take a look:
sa: matrix[op] [ a ] = [ 1.00 0 0 ] [ a ] [ b ] [ 2.00 0.50 2.00 ] [ b ] [ c ] [ 3.00 9.00 0 ] [ c ] [ e ] [ 0 5.00 7.00 ] |matrix>
-- and we finish with a slightly more interesting function, the train-of-thought function.
-- this code makes heavy use of supported-ops, pick-elt and apply().
-- and will work much better with a big knowledge base, but even a small one gives hints of what a large example will be like.
sa: load early-us-presidents.sw -- load up some knowledge
sa: create inverse -- needed, else we run into dead ends.
sa: train-of-thought[13] |Madison> -- take 13 steps, starting with |Madison>
context: sw console
one: |Madison>
n: 13
|X>: |Madison>
|early US Presidents: _list>
|Adams>
|year: 1797>
|Washington>
|early US Presidents: _list>
|Adams>
|number: 2>
|Adams>
|year: 1801>
|Jefferson>
|early US Presidents: _list>
|Adams>
|year: 1799>
Anyway, I guess the summary of this post is that we have some proof of concept functions trying to map our BKO scheme towards a more general purpose knowledge engine. Don't take the above functions as finished, take them as hints on where we could take this project.
Tuesday, 6 January 2015
introducing sigmoids
Now, next thing we need to mention are what I call "sigmoids". They are functions that you apply to superpositions and they only change the coeffs in superpositions. They do not, by themselves, change the order or labels of kets in superpositions. Named loosely after these guys.
-- set all coeffs above 0 to 1, else 0
clean SP
-- set everything below t to 0, else x
-- similar to drop-below[t]
threshold-filter[t] SP
-- set everything below t to x, else 0
-- similar to drop-above[t]
not-threshold-filter[t] SP
-- set everything below 0.96 to 0, else 1
binary-filter SP
-- set everything below 0.96 to 1, else 0
not-binary-filter SP
-- set everything below 0 to 0, else x
pos SP
-- return the absolute value of x
abs SP
-- set everything above t to t, else x
max-filter[t] SP
-- set everything below 0.04 to 1, else 0
NOT SP
-- set everything in range [0.96,1.04] to 1, else 0
xor-filter SP
-- set everything in range [a,b] to x, else 0
sigmoid-in-range[a,b] SP
-- set all coeffs to 1/x. if x == 0, then return 0
invert SP
-- set all coeffs to t - x
subtraction-invert[t] SP
-- sets all coeffs, including zeros, to t
set-to[t] SP
They are simple enough, so here is the python:
So, that is it for now. Heaps more function operators to come!
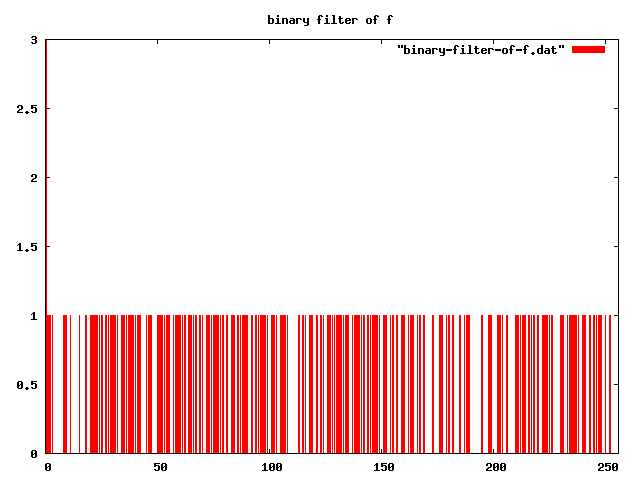
Update: Here is a visualization of a couple of sigmoids in action:
-- define a function, with values in [0,3]
-- NB: the multiply by 0 is in there, else it would be in range [1,4] since the noise is additive
|f> => absolute-noise[3] 0 range(|x: 0>,|x: 255>)
-- apply binary filter to that function:
-- NB: I set |x: 0> to 3, so graph y-axis wasn't auto-scaled to [0,1]
binary-filter "" |f>
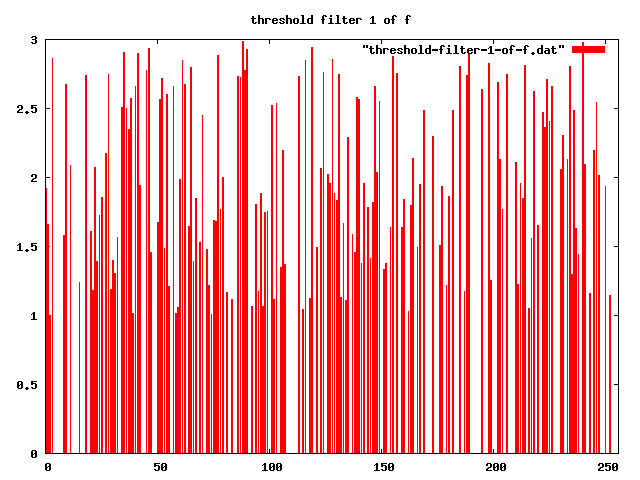
-- apply threshold-filter, with t = 1
threshold-filter[1] "" |f>
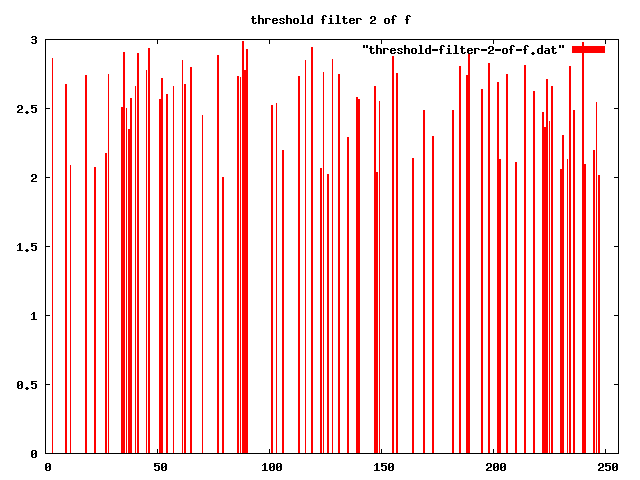
-- apply threshold-filter, with t = 2
threshold-filter[2] "" |f>
-- apply threshold-filter, with t = 2.5
threshold-filter[2.5] "" |f>
-- set all coeffs above 0 to 1, else 0
clean SP
-- set everything below t to 0, else x
-- similar to drop-below[t]
threshold-filter[t] SP
-- set everything below t to x, else 0
-- similar to drop-above[t]
not-threshold-filter[t] SP
-- set everything below 0.96 to 0, else 1
binary-filter SP
-- set everything below 0.96 to 1, else 0
not-binary-filter SP
-- set everything below 0 to 0, else x
pos SP
-- return the absolute value of x
abs SP
-- set everything above t to t, else x
max-filter[t] SP
-- set everything below 0.04 to 1, else 0
NOT SP
-- set everything in range [0.96,1.04] to 1, else 0
xor-filter SP
-- set everything in range [a,b] to x, else 0
sigmoid-in-range[a,b] SP
-- set all coeffs to 1/x. if x == 0, then return 0
invert SP
-- set all coeffs to t - x
subtraction-invert[t] SP
-- sets all coeffs, including zeros, to t
set-to[t] SP
They are simple enough, so here is the python:
def clean(x):
if x <= 0:
return 0
else:
return 1
def threshold_filter(x,t):
if x < t:
return 0
else:
return x
def not_threshold_filter(x,t):
if x <= t:
return x
else:
return 0
def binary_filter(x):
if x <= 0.96:
return 0
else:
return 1
def not_binary_filter(x):
if x <= 0.96:
return 1
else:
return 0
def pos(x):
if x <= 0:
return 0
else:
return x
def sigmoid_abs(x):
return abs(x)
def max_filter(x,t):
if x <= t:
return x
else:
return t
def NOT(x):
if x <= 0.04:
return 1
else:
return 0
# otherwise known as the Goldilock's function.
# not too hot, not too cold.
def xor_filter(x):
if 0.96 <= x and x <= 1.04:
return 1
else:
return 0
# this is another type of "Goldilock function"
# the in-range sigmoid:
def sigmoid_in_range(x,a,b):
if a <= x and x <= b:
return x
else:
return 0
def invert(x):
if x == 0:
return 0
else:
return 1/x
def subtraction_invert(x,t):
return t - x
def set_to(x,t):
return t
Sigmoids are simple and tidy enough, so if it turns out we need a new one, it will be fine to add it. This is in contrast with ket/sp built in functions, where we are reluctant to add new functions unless there is no neater way to do it.So, that is it for now. Heaps more function operators to come!
Update: Here is a visualization of a couple of sigmoids in action:
-- define a function, with values in [0,3]
-- NB: the multiply by 0 is in there, else it would be in range [1,4] since the noise is additive
|f> => absolute-noise[3] 0 range(|x: 0>,|x: 255>)
-- apply binary filter to that function:
-- NB: I set |x: 0> to 3, so graph y-axis wasn't auto-scaled to [0,1]
binary-filter "" |f>
-- apply threshold-filter, with t = 1
threshold-filter[1] "" |f>
-- apply threshold-filter, with t = 2
threshold-filter[2] "" |f>
-- apply threshold-filter, with t = 2.5
threshold-filter[2.5] "" |f>
some built in functions
First up in phase 2, some functions built into our ket and superposition classes. There are quite a few of these, but in this post I think I will only mention the most useful ones. (note that SP is just some superposition)
-- randomly select an element from SP
-- eventually I want a weighted pick-elt too.
pick-elt SP
-- normalize so sum of coeffs = 1
-- (this can be used to map a frequency list to a list of probabilities)
normalize SP
-- normalize so sum of coeffs = t
normalize[t] SP
-- rescale coeffs so coeff of max element = 1
rescale SP
-- rescale coeffs so coeff of max element = t
rescale[t] SP
--returns number of elements in SP in |number: x> format
count SP
how-many SP
-- returns sum of coeffs of the elements in SP in |number: x> format
count-sum SP
sum SP
-- returns the product of coeffs of the elements in SP in |number: x> format
product SP
-- drop elements from SP with coeff <= 0.
-- NB: in our model coeffs are almost always >= 0
drop SP
-- drop elements from SP with coeff below t
drop-below[t] SP
-- drop elements from SP with coeff above t
drop-above[t] SP
-- keep elements with index in range [a,b]
-- NB: index starts at 1, not 0
select-range[a,b] SP
select[a,b] SP
-- return element with index k
select-elt[k] SP
-- delete k'th element from the superposition.
delete-elt[k] SP
-- reverse the SP
reverse SP
-- shuffle the SP
shuffle SP
-- sort superposition by the coeffs of the kets
-- this one is very useful!
-- especially in combination with op-self operators
coeff-sort SP
-- sort using a natural sort of lowercase labels of the kets
-- NB: sometimes natural sort bugs out, and I have to manually
-- swap the code back to standard lowercase sort.
-- eg, the binary tree example with kets such as |00> and |0010> and so on.
ket-sort SP
-- return the first ket found with the max coeff
max-elt SP
-- return the first ket found with the min coeff
min-elt SP
-- return the kets with the max coeff
max SP
-- return the kets with the min coeff
min SP
-- return the max coeff in the SP in |number: x> format
max-coeff SP
-- return the min coeff in the SP in |number: x> format
min-coeff SP
-- mulitply all coeffs by t
mult[t] SP
-- add noise to the SP in range [0,t]
absolute-noise[t] SP
-- add noise to the SP in range [0,t*max_coeff]
relative-noise[t] SP
-- returns the difference between the largest coeff and the second largest coeff.
-- in 3| > format.
discrimination SP
discrim SP
-- returns |no> if SP is the identity element |>
-- otherwise returns |yes>
not-empty SP
do-you-know SP
I guess that is about it! Note there is a longer, more detailed version of the above here, which shows the mapping between the underlying python and the BKO (though it is incomplete).
BTW, I deliberately left out these two, as I will describe them in phase 3 of the write-up:
similar[op] |x>
find-topic[op] |x>
-- randomly select an element from SP
-- eventually I want a weighted pick-elt too.
pick-elt SP
-- normalize so sum of coeffs = 1
-- (this can be used to map a frequency list to a list of probabilities)
normalize SP
-- normalize so sum of coeffs = t
normalize[t] SP
-- rescale coeffs so coeff of max element = 1
rescale SP
-- rescale coeffs so coeff of max element = t
rescale[t] SP
--returns number of elements in SP in |number: x> format
count SP
how-many SP
-- returns sum of coeffs of the elements in SP in |number: x> format
count-sum SP
sum SP
-- returns the product of coeffs of the elements in SP in |number: x> format
product SP
-- drop elements from SP with coeff <= 0.
-- NB: in our model coeffs are almost always >= 0
drop SP
-- drop elements from SP with coeff below t
drop-below[t] SP
-- drop elements from SP with coeff above t
drop-above[t] SP
-- keep elements with index in range [a,b]
-- NB: index starts at 1, not 0
select-range[a,b] SP
select[a,b] SP
-- return element with index k
select-elt[k] SP
-- delete k'th element from the superposition.
delete-elt[k] SP
-- reverse the SP
reverse SP
-- shuffle the SP
shuffle SP
-- sort superposition by the coeffs of the kets
-- this one is very useful!
-- especially in combination with op-self operators
coeff-sort SP
-- sort using a natural sort of lowercase labels of the kets
-- NB: sometimes natural sort bugs out, and I have to manually
-- swap the code back to standard lowercase sort.
-- eg, the binary tree example with kets such as |00> and |0010> and so on.
ket-sort SP
-- return the first ket found with the max coeff
max-elt SP
-- return the first ket found with the min coeff
min-elt SP
-- return the kets with the max coeff
max SP
-- return the kets with the min coeff
min SP
-- return the max coeff in the SP in |number: x> format
max-coeff SP
-- return the min coeff in the SP in |number: x> format
min-coeff SP
-- mulitply all coeffs by t
mult[t] SP
-- add noise to the SP in range [0,t]
absolute-noise[t] SP
-- add noise to the SP in range [0,t*max_coeff]
relative-noise[t] SP
-- returns the difference between the largest coeff and the second largest coeff.
-- in 3| > format.
discrimination SP
discrim SP
-- returns |no> if SP is the identity element |>
-- otherwise returns |yes>
not-empty SP
do-you-know SP
I guess that is about it! Note there is a longer, more detailed version of the above here, which shows the mapping between the underlying python and the BKO (though it is incomplete).
BTW, I deliberately left out these two, as I will describe them in phase 3 of the write-up:
similar[op] |x>
find-topic[op] |x>
Sunday, 4 January 2015
Announcing phase 2: function operators
Now, with phase 1 out of the way, I can move on to phase 2. Phase 1 was largely about literal operators, ie those defined in a learn rule: OP KET => SUPERPOSITION. But so far I have only hinted that there is also a large collection of function operators, operators that do some processing, eg, mentioned so far: pick-elt, normalize, algebra, and a couple of others.
Subscribe to:
Posts (Atom)