-- set all coeffs above 0 to 1, else 0
clean SP
-- set everything below t to 0, else x
-- similar to drop-below[t]
threshold-filter[t] SP
-- set everything below t to x, else 0
-- similar to drop-above[t]
not-threshold-filter[t] SP
-- set everything below 0.96 to 0, else 1
binary-filter SP
-- set everything below 0.96 to 1, else 0
not-binary-filter SP
-- set everything below 0 to 0, else x
pos SP
-- return the absolute value of x
abs SP
-- set everything above t to t, else x
max-filter[t] SP
-- set everything below 0.04 to 1, else 0
NOT SP
-- set everything in range [0.96,1.04] to 1, else 0
xor-filter SP
-- set everything in range [a,b] to x, else 0
sigmoid-in-range[a,b] SP
-- set all coeffs to 1/x. if x == 0, then return 0
invert SP
-- set all coeffs to t - x
subtraction-invert[t] SP
-- sets all coeffs, including zeros, to t
set-to[t] SP
They are simple enough, so here is the python:
def clean(x):
if x <= 0:
return 0
else:
return 1
def threshold_filter(x,t):
if x < t:
return 0
else:
return x
def not_threshold_filter(x,t):
if x <= t:
return x
else:
return 0
def binary_filter(x):
if x <= 0.96:
return 0
else:
return 1
def not_binary_filter(x):
if x <= 0.96:
return 1
else:
return 0
def pos(x):
if x <= 0:
return 0
else:
return x
def sigmoid_abs(x):
return abs(x)
def max_filter(x,t):
if x <= t:
return x
else:
return t
def NOT(x):
if x <= 0.04:
return 1
else:
return 0
# otherwise known as the Goldilock's function.
# not too hot, not too cold.
def xor_filter(x):
if 0.96 <= x and x <= 1.04:
return 1
else:
return 0
# this is another type of "Goldilock function"
# the in-range sigmoid:
def sigmoid_in_range(x,a,b):
if a <= x and x <= b:
return x
else:
return 0
def invert(x):
if x == 0:
return 0
else:
return 1/x
def subtraction_invert(x,t):
return t - x
def set_to(x,t):
return t
Sigmoids are simple and tidy enough, so if it turns out we need a new one, it will be fine to add it. This is in contrast with ket/sp built in functions, where we are reluctant to add new functions unless there is no neater way to do it.So, that is it for now. Heaps more function operators to come!
Update: Here is a visualization of a couple of sigmoids in action:
-- define a function, with values in [0,3]
-- NB: the multiply by 0 is in there, else it would be in range [1,4] since the noise is additive
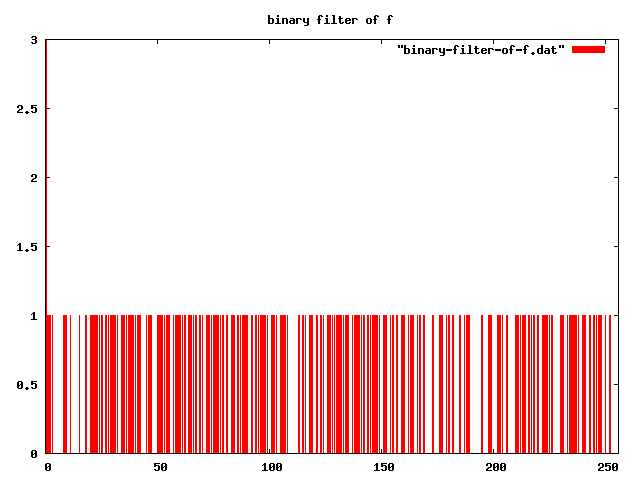
|f> => absolute-noise[3] 0 range(|x: 0>,|x: 255>)
-- apply binary filter to that function:
-- NB: I set |x: 0> to 3, so graph y-axis wasn't auto-scaled to [0,1]
binary-filter "" |f>
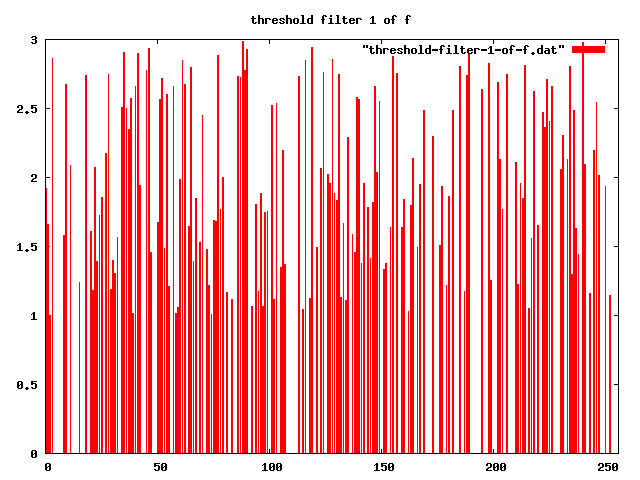
-- apply threshold-filter, with t = 1
threshold-filter[1] "" |f>
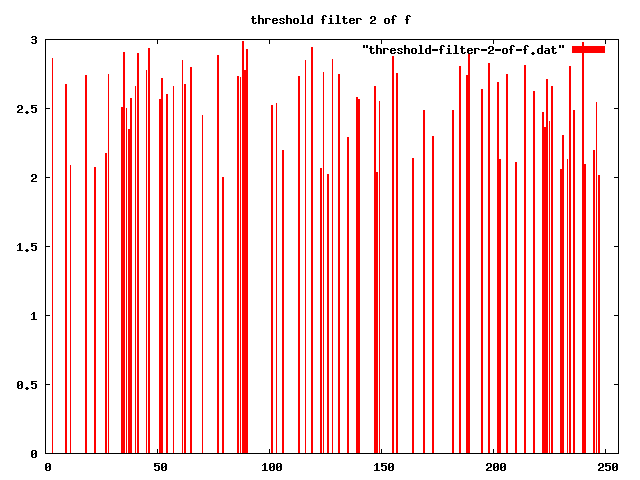
-- apply threshold-filter, with t = 2
threshold-filter[2] "" |f>
-- apply threshold-filter, with t = 2.5
threshold-filter[2.5] "" |f>


No comments:
Post a Comment