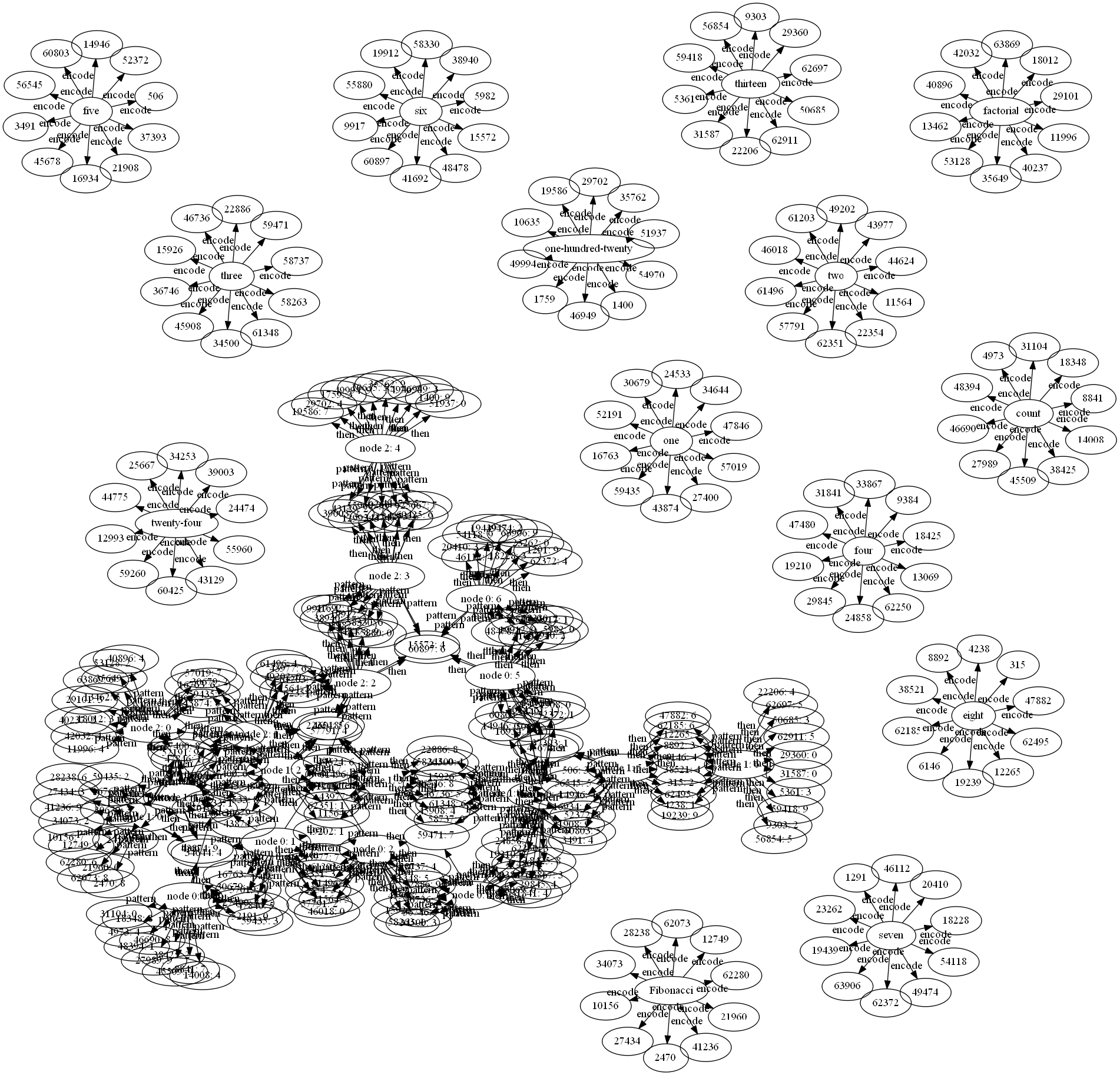
Let's jump right in. In the first couple of examples, we use 10 on bits, and column-size 10:
-- define our first set of sequences: "count one two three four five six seven", "Fibonacci one one two three five eight thirteen", "factorial one two six twenty-four one-hundred-twenty" -- run the code: $ ./learn-high-order-sequences.pyAnd now we have this file. After loading that file, saving it and manually removing the learn rules we don't want in our visualization (eg, full |range>, sequence-number, and our operators), we have this file. Feed that to sw2dot-v2.py and graphviz:
Now, let's try to explain this image. The individual isolated circles correspond to the encode learn rules:
encode |two> => pick[10] full |range> encode |three> => pick[10] full |range> encode |four> => pick[10] full |range> encode |five> => pick[10] full |range>The chain like thing is our sequences. But since they are so short, and have a lot of overlap they are all tangled together. Which inspired the next example, one long single sequence:
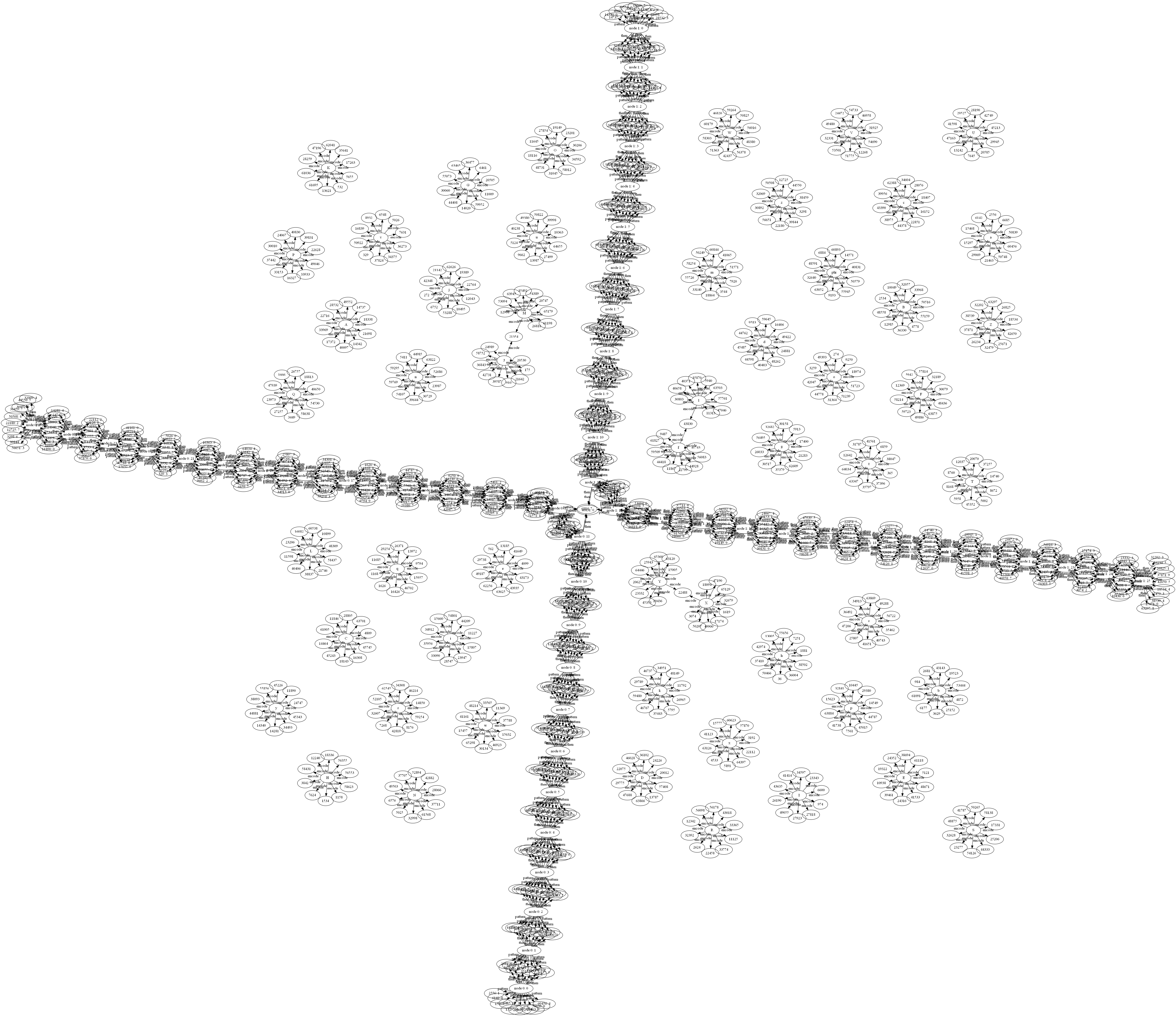
"a b c d e f g h i j k l m n o p q r s t u v w x y z"One end of this chain corresponds to "a", the other end to "z", obviously. The joins correspond to places where the superpositions have overlap. ie these learn rules:
pattern |node 0: 0> => random-column[10] encode |a> then |node 0: 0> => random-column[10] encode |b> pattern |node 0: 1> => then |node 0: 0> then |node 0: 1> => random-column[10] encode |c> pattern |node 0: 2> => then |node 0: 1> then |node 0: 2> => random-column[10] encode |d> ...Now, some more examples. Here is the lower and uppercase alphabets with a single meeting point "phi" in the middle:
"a b c d e f g h i j k l phi m n o p q r s t u v w x y z" "A B C D E F G H I J K L phi M N O P Q R S T U V W X Y Z"Next, the alphabets plus a joining bridge (even if it didn't join in the right spot):
"a b c d e f g h i j k l phi-0 m n o p q r s t u v w x y z" "A B C D E F G H I J K L phi-5 M N O P Q R S T U V W X Y Z" "phi-0 phi-1 phi-2 phi-3 phi-4 phi-5"Next, a repeated sequence, in this case the lowercase alphabet repeated twice:
"a b c d e f g h i j k l m n o p q r s t u v w x y z" "a b c d e f g h i j k l m n o p q r s t u v w x y z"I had expected this one to be two separate chains, but I guess due to noise there is some overlap in the representations for each letter. If we repeat this example, but with column size ramped up to 50, we get less overlap:
OK. Now I want to know what column size I need for there to be no ket overlaps in our representations. Here is column size 100, which is getting closer, now with only a couple of overlaps:
Finally! Column size 200 produces two fully independent sequences for our repeated alphabet:
You would think it would be easy to choose a shape and then define a collection of sequences that will produce that shape. Heh, due to the random nature of these things, not so much. eg, it took me several tries to make a triangle that overlapped in just the right spots. Even then it returned a circle, not the desired triangle. Here are my sequences:
"a b c d e f g h i j k l m n o p q r s t u v w x y z" "a b1 c1 d1 e1 f1 g1 h1 i1 j1 k1 l1 m1 n1 o1 p1 q1 r1 s1 t1 u1 v1 w1 x1 y1 z1" "z1 b2 c2 d2 e2 f2 g2 h2 i2 j2 k2 l2 m2 n2 o2 p2 q2 r2 s2 t2 u2 v2 w2 x2 y2 zAnd here is my "triangle":
A nice demonstration of how randomness effects these things. Here are the same set of sequences, but this time 40 instead of 10 on bits, with column size still 10:
Looks completely different, though interestingly, with the 40 on bits, these things are starting to look like molecules. Which kind of makes sense, if we use the rough analogy of mapping kets to electron orbit positions. But without more work, this is just a rough analogy. There are plenty of differences between those two systems.








No comments:
Post a Comment