Formally, the problem of supervised pattern recognition can be stated as follows: Given an unknown function
 (the ground truth) that maps input instances
(the ground truth) that maps input instances  to output labels
to output labels  , along with training data
, along with training data  assumed to represent accurate examples of the mapping, produce a function
assumed to represent accurate examples of the mapping, produce a function 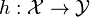 that approximates as closely as possible the correct mapping
that approximates as closely as possible the correct mapping  .
.Now, I have been making claims about pattern recognition using my similar[op]. Let me show that we can actually do this with the BKO scheme:
Here is the training data for AND (and we will use the convention that x0 is always 1):
(1,0,0),0
(1,0,1),0
(1,1,0),0
(1,1,1),1
-- now, let's encode that in BKO: -- NB: if a ket has 0 for coeff we don't include them in our superpositions. pattern |a> => |x0> pattern |b> => |x0> + |x2> pattern |c> => |x0> + |x1> pattern |d> => |x0> + |x1> + |x2> M |a> => |0> M |b> => |0> M |c> => |0> M |d> => |1> -- now define some example input patterns: input-pattern |u> => |x0> input-pattern |v> => |x0> + |x2> input-pattern |x> => |x0> + |x1> input-pattern |y> => |x0> + |x1> + |x2> -- now define our h: h |*> #=> M drop-below[0.7] similar[input-pattern,pattern] |_self> -- now take a look at the table: sa: table[input,h] (|u> + |v> + |x> + |y>) +-------+---+ | input | h | +-------+---+ | u | 0 | | v | 0 | | x | 0 | | y | 1 | +-------+---+It worked!
Here is the training data for NAND from here:
(1,0,0),1
(1,0,1),1
(1,1,0),1
(1,1,1),0
-- now, let's encode that in BKO: pattern |a> => |x0> pattern |b> => |x0> + |x2> pattern |c> => |x0> + |x1> pattern |d> => |x0> + |x1> + |x2> M |a> => |1> M |b> => |1> M |c> => |1> M |d> => |0> -- now define some example input patterns: input-pattern |u> => |x0> input-pattern |v> => |x0> + |x2> input-pattern |x> => |x0> + |x1> input-pattern |y> => |x0> + |x1> + |x2> -- now take a look at the table: -- NB: split is just to save typing sa: table[input,h] split |u v x y> +-------+---+ | input | h | +-------+---+ | u | 1 | | v | 1 | | x | 1 | | y | 0 | +-------+---+Again, it worked!
And finally, the cool one! XOR is meant to be hard, but we can do it in our scheme.
Here is the training data for XOR:
(1,1,0),1
(1,0,1),1
(1,0,0),0
(1,1,1),0
-- now let's encode that in BKO: pattern |a> => |x0> + |x1> pattern |b> => |x0> + |x2> pattern |c> => |x0> pattern |d> => |x0> + |x1> + |x2> M |a> => |1> M |b> => |1> M |c> => |0> M |d> => |0> -- now define some example input patterns: input-pattern |u> => |x0> + |x1> input-pattern |v> => |x0> + |x2> input-pattern |x> => |x0> input-pattern |y> => |x0> + |x1> + |x2> -- now take a look at the table: sa: table[input,h] split |u v x y> +-------+---+ | input | h | +-------+---+ | u | 1 | | v | 1 | | x | 0 | | y | 0 | +-------+---+Again, it worked!!
Now for a sample test case where the pattern is not an exact match:
sa: input-pattern |z> => 0.7|x0> + 0.900|x1> + 0.85|x2> sa: table[input,h] split |u v x y z> +-------+--------+ | input | h | +-------+--------+ | u | 1 | | v | 1 | | x | 0 | | y | 0 | | z | 0.95 0 | +-------+--------+ie, z is a 95% match with |0>
Now, look at the underlying similarity values:
sa: foo |*> #=> 100 similar[input-pattern,pattern] |_self> sa: table[input,foo] split |u v x y z> +-------+------------------------------------+ | input | foo | +-------+------------------------------------+ | u | 100 a, 66.67 d, 50 b, 50 c | | v | 100 b, 66.67 d, 50 a, 50 c | | x | 100 c, 50 a, 50 b, 33.33 d | | y | 100 d, 66.67 a, 66.67 b, 33.33 c | | z | 95.24 d, 65.31 a, 63.27 b, 28.57 c | +-------+------------------------------------+And some notes:
1) it should be obvious that if it works for one logic case it will work for all cases. Why? Well, the detection of the logic state (ie, the similar[op] bit) is independent of the apply label stage (ie, the M |a> => ...).
2) we have only 1 parameter to tweak, the value we use in drop-below[] that decides how close to the original pattern the incoming pattern has to be, before we ignore it. But for now drop-below[0.7] (ie 70% similarity) should probably do. Though we could also swap in a sigmoid if we want.
3) I guess you could call this version "inclusive matching". A node does not "care" if its neighbour nodes are firing. In "exclusive matching" a node will try to suppress the firing of neighbouring nodes.
4) the method is perfectly general. If we cast our training data to superpositions, and use this general training data:
D = {(X1,Y1),(X2,Y2),...(Xn,Yn)}
where Xi, and Yi are superpositions.
Then simply enough:
pattern |node: 1> => X1
pattern |node: 2> => X2
...
pattern |node: n> => Xn
M |node: 1> => Y1
M |node: 2> => Y2
...
M |node: n> => Yn
-- define our h:
h |*> #=> M drop-below[0.7] similar[input-pattern,pattern] |_self>
And that should be it! The only thing is we need to take care if Xi or Yi are superpositions with all coeffs 0, in which case we would need to do some massaging. Besides, who inputs "nothing" and expects to get out "something"?
Seriously cool! And BTW, similar[op] is biologically plausible in terms of neurons. I'll show how in phase 4.
Update: let's redo this, and tidy up the logic example a little.
Define our patterns we want to match:
(1,0,0) (1,0,1) (1,1,0) (1,1,1)Then in BKO:
pattern |a> => |x0> + 0|x1> + 0|x2> pattern |b> => |x0> + 0|x1> + |x2> pattern |c> => |x0> + |x1> + 0|x2> pattern |d> => |x0> + |x1> + |x2>Now define our labels:
OR-label |a> => |0> OR-label |b> => |1> OR-label |c> => |1> OR-label |d> => |1> XOR-label |a> => |0> XOR-label |b> => |1> XOR-label |c> => |1> XOR-label |d> => |0> AND-label |a> => |0> AND-label |b> => |0> AND-label |c> => |0> AND-label |d> => |1>Now define some example input patterns:
input-pattern |u> => |x0> + 0|x1> + 0|x2> input-pattern |v> => |x0> + 0|x1> + |x2> input-pattern |x> => |x0> + |x1> + 0|x2> input-pattern |y> => |x0> + |x1> + |x2>Now define our logic operators:
OR |*> #=> OR-label drop-below[0.7] similar[input-pattern,pattern] |_self> XOR |*> #=> XOR-label drop-below[0.7] similar[input-pattern,pattern] |_self> AND |*> #=> AND-label drop-below[0.7] similar[input-pattern,pattern] |_self>Now take a look at the resulting table:
sa: table[input,OR,XOR,AND] split |u v x y> +-------+----+-----+-----+ | input | OR | XOR | AND | +-------+----+-----+-----+ | u | 0 | 0 | 0 | | v | 1 | 1 | 0 | | x | 1 | 1 | 0 | | y | 1 | 0 | 1 | +-------+----+-----+-----+So we are matching our input patterns (u, v, x and y) against our stored patterns (a, b, c and d), and then the logic operators (OR, XOR, AND) choose what logic labels (OR-label, XOR-label, AND-label) to apply to those patterns.
The resulting sw file is here.
Update: Alternatively, we can use True/False. We could define a whole new set of OR-label, XOR-label and AND-label, but it is shorter to just do this:
TF |0> => |False> TF |1> => |True> TF-OR |*> #=> TF OR |_self> TF-XOR |*> #=> TF XOR |_self> TF-AND |*> #=> TF AND |_self>Now take a look at the resulting table:
sa: table[input,TF-OR,TF-XOR,TF-AND] split |u v x y> +-------+-------+--------+--------+ | input | TF-OR | TF-XOR | TF-AND | +-------+-------+--------+--------+ | u | False | False | False | | v | True | True | False | | x | True | True | False | | y | True | False | True | +-------+-------+--------+--------+Cool! And it didn't take much work. In the BKO scheme, renaming kets is quite often very simple and easy to do.
I only understand the definition from wikipedia but NOT the rest of this post :(
ReplyDelete